Лаборатория математического моделирования нелинейных динамических систем основана в 2014 году.
Основные направления исследований сотрудников лаборатории:
- локализация инвариантных компактов непрерывных и дискретных динамических систем, хаотическая динамика;
- исследование непрерывных и дискретных нелинейных динамических систем и процессов управления на основе алгебраических и дифференциально-геометрических методов и разработка для них алгоритмов управления;
- исследование устойчивости, построение областей притяжения и поиск функций Ляпунова для нелинейных систем;
 - изучение неминимально фазовых систем, математическое моделирование процессов управления нелинейными системами;
- изучение неминимально фазовых систем, математическое моделирование процессов управления нелинейными системами;
- геометрия систем с запаздыванием, систем интегро-дифференциальных уравнений и других типов систем, имеющих гранично-дифференциальную форму;
- вычисление и использование в прикладных исследованиях симметрии, интегрируемых симметрий, законов сохранения и преобразований таких систем, а также динамических систем с управлением;
- обратимые дифференциальные операторы;
- задача плоскостности динамических систем с управлением, систем с запаздыванием и систем с распределенными параметрами;
- решение задачи путевой стабилизации колесных роботов;
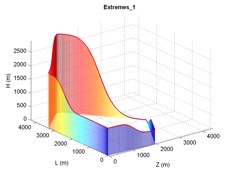
- проектирование сложных пространственных маневров для летательных аппаратов;
 - моделирование работы лабораторного робота с использованием системы технического зрения;
- моделирование работы лабораторного робота с использованием системы технического зрения;
- моделирование вращения космического аппарата вокруг центра масс;
- моделирование поведения колесного робота в условиях неопределенности.
Важнейшие результаты, полученные сотрудниками лаборатории:
- доказаны условия асимптотической устойчивости и асимптотической устойчивости в целом в терминах инвариантных компактов и положительно инвариантных множеств;
- описано поведение траекторий автономных и неавтономных систем дифференциальных уравнений вне локализирующих множеств, соответствующих локализирующим функциям;
 - функциональный метод локализации инвариантных компактных множеств распространен на семейства дискретных динамических систем;
- функциональный метод локализации инвариантных компактных множеств распространен на семейства дискретных динамических систем;
- разработан новый метод построения функций Ляпунова для доказательства асимптотической устойчивости положений равновесия динамических систем;
- функциональный метод локализации инвариантных компактных множеств распространен на дифференциальные включения;
- решена задача локализации управляемо робастно инвариантных компактных множеств непрерывных и дискретных динамических систем с возмущением и управлением.




