В задачах курсовых заданий на сложное движение точки применяются теоремы о сложении скоростей и ускорений, и студенты обучаются методам вычисления скоростей и ускорений точек с помощью этих теорем.
Условно задачи на сложное движение точки можно представить как задачи двух видов – «прямые» и «обратные». В прямых задачах по известному закону относительного движения точки и параметрам переносного движения требуется найти абсолютные скорость и ускорение точки. Эти задачи студенты, как правило, быстро воспринимают и умеют хорошо решать. К «обратным» можно отнести те задачи, в которых известна абсолютная траектория точки. Требуется найти кинематические характеристики, оставшиеся неизвестными в абсолютном, относительном или переносном движениях. Такие задачи вызывают у студентов много вопросов и решаются хуже, чем «прямые». Поэтому в заданиях для студентов долго преобладали «прямые» задачи.
Методика решения «прямых» задач с переносными вращательным и поступательным движениями изложена в учебном пособии «Решение задач по кинематике» Л. Г. Тихоновой и Т. И. Гориной (Изд. МВТУ, 1967)
В 1973 г. опубликовано учебное пособие по кинематике, содержащее варианты «прямых» и «обратных» задач сложного движения точки (Кинематика точки. Кинематика простейших движений твердого тела. Кинематика сложного движения точки. Авторы: В. К. Бочаров, Б. А. Бурмистров, К. И. Иванова, И. С. Козлов, В. П. Кутлер).
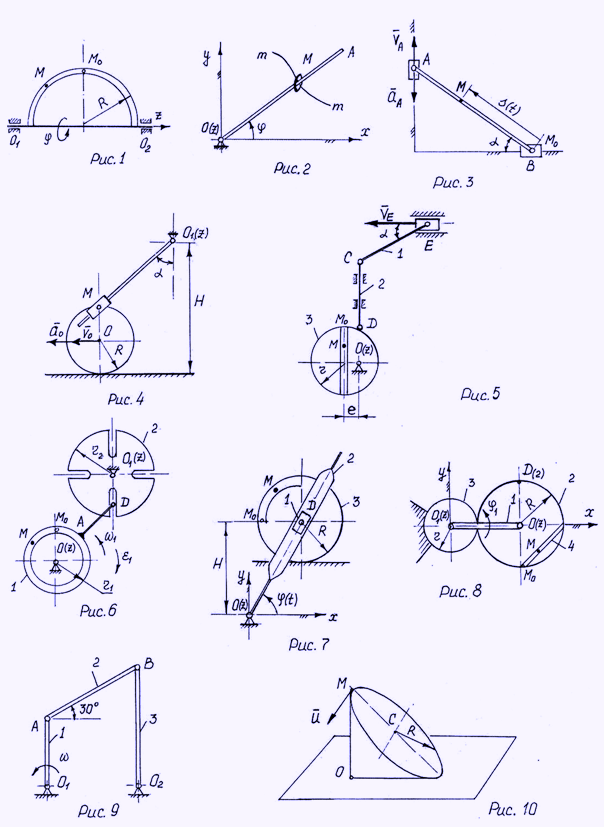
В «прямых» задачах использованы как традиционные в то время схемы с переносным вращательным движением (рис. 1) (см. «Сборник заданий для курсовых работ по теоретической механике под ред. А. А. Яблонского. – М.: Высшая школа, 1972), так и задачи с переносным плоским движением – их еще только две. В «обратных» задачах представлено несколько схем кулисных механизмов, обращенного эллиптического циркуля, а также задачи, которые показаны на рис. 2.
Кольцо М (материальная точка), надетое на стержень ОА, движется по траектории m – m в плоскости хОу, вращая стержень вокруг оси O(z). Заданы уравнения движения точки M x=x(t), y=y(t), задано ее начальное положение (при t=0). Требуется определить при t=t1 угловые скорость и ускорение стержня ОА, а также относительные (по отношению к стержню) скорость и ускорение точки М. Методика решения такого вида задач (рис. 2), а также решение «прямых» задач содержатся в методических указаниях по выполнению этого задания (Е. С. Веселый, П. В. Занозин, Л. Е. Ефремова, Б. А. Бурмистров «Статика – кинематика», изд. МВТУ, 1974). В это же время изданы и методические указания для студентов вечернего факультета, содержащие исключительно «прямые» задачи с переносным вращательным движением с подробными пояснениями и примерами решения (1974 г. под ред. В. П Трониной, авторы – В. П. Тронина, Н. И. Виляевская, Г. Ф Ефремов; и в 1982 г. – с большим количеством новых вариантов – В. П. Тронина, Ю. Д. Плешаков, Г. М. Тушева).
В 1980 г. для студентов дневных факультетов издано методическое пособие, содержащее 36 вариантов курсового задания, каждый из которых состоял из «прямой» и «обратной» задач (П. В. Занозин, Н. Н. Пилюгина, Г. М. Тушева «Кинематика сложного движения точки». МВТУ).
Здесь из 72-х задач 11 включали звенья с плоским движением как в «прямых» (рис. 3), так и в «обратных» задачах (рис. 4).
По заказу министерства высшего образования СССР через НПО «Союз-вузприбор» в 1983 г. была издана обучающая программа по теме «Кинематика сложного движения точки» объемом в 80 кадров (авторы: З. И. Тихонова и Г. М. Тушева). Программа предназначалась для студентов технических вузов страны и содержала методику и примеры решения «прямых» и «обратных» задач.
Обобщением накопленного опыта по методике решения задач явились «Методические указания к выполнению курсовой работы и решению задач по теме «Кинематика сложного движения точки», изданные в 1985 г. под ред. К.С. Колесникова (авторы: Дубинин В. В., Занозин П. В., Солохин Е. Н., Орфаницкая Л. П.), изд. МВТУ. Здесь проведена четкая классификация задач, рассмотрены все случаи относительного и переносного движений, даны необходимые пояснения и многочисленные примеры: 36 решений и 16 задач для самостоятельных практических занятий.
Качественно новый подход к структуре вариантов задания по сложному движению точки содержится в методических указаниях, изданных в1987 г. (Кинематика плоского движения твердого тела. Кинематика сложного движения точки под ред. К. С. Колесникова. Авторы: В. В. Дубинин, Г. Ф. Ефремов, А. И. Пастухов. Изд. МВТУ).
Схема каждого из 32-х вариантов теперь представляет собой комплекс из двух задач – из «прямой» для точки М и «обратной» для точки D. В большинстве вариантов сначала решается «обратная» задача – при известном абсолютном движении точки D механизма получить угловые скорость и ускорение звена, несущего на себе подвижную точку М (рис. 5). Затем рассматривается «прямая» задача, в которой определяются абсолютные скорость и ускорение точки М, относительное движение которой задано. Часть задач (рис. 6) решается в любом порядке.
Для промежуточного контроля знаний студентов в 1990 г. составлены и тиражированы 32 варианта «прямых» и «обратных» задач экзаменационной сложности (Материалы для КСР по теме «Кинематика сложного движения точки», авторы М. М. Ильин и Г. М. Тушева).
В 1997 г. были подготовлены к изданию в редакции МГТУ материалы методических указаний и новой редакции вариантов курсовой работы по теме «Сложное движение точки». Авторы: Дубинин В. В., Гатауллина Г. И., Тушева Г. М. и Ремизов А. В. Работа содержит теперь 44 варианта комплексных задач с использованием самых разнообразных плоских и пространственных механизмов. Это дает возможность преподавателю, ведущему практические занятия в группах, выбрать для каждого студента наиболее подходящий вариант.
Больше половины схем вариантов – новые задачи. По-прежнему, для точки D решается «обратная» задача, а затем для точки М – «прямая» (рис. 7). Введены задачи «обратного» типа, в которых назначается подвижная система отсчета и требуется найти относительные скорость и ускорение точки D(2) (звено 2) относительно звена 1, с которым связана подвижная система отсчета.
Так, в планетарном механизме (рис. 8) кривошип 1, вращаясь вокруг оси О1(z) неподвижной шестерни 3, приводит в движение шестеренку 2. Связав с кривошипом 1 подвижную систему отсчета хО1у , нужно найти для точки D(2) шестерни 2 относительные скорость и ускорение. Для точки М, которая движется вдоль паза 4 на шестерне 2, задано относительное движение, требуется найти абсолютные скорость и ускорение.
Предусмотрено выполнение каждого варианта задания с помощью ЭВМ – для разных положений механизма можно в диапазоне времени 0 ≤t ≤ 1 с получить характеристики относительного, переносного и абсолютного движений точек М и D.
В 2001 г. подготовлены к печати в редакции МГТУ «Методические указания по выполнению задания и решению задач по теме «Кинематика сложного движения точки» – авторы: Дубинин В. В., Гатауллина Г. И., Тушева Г. М.
В последние годы на кафедре проводится работа по составлению задачника для подготовки студентов к олимпиадам по теоретической механике. В разделе «Сложное движение точки» систематизированы и разобраны наиболее интересные задачи прошедших олимпиад. В задачнике представлены и короткие задачи, которые, как известно, очень эффективно используются в учебных и контрольных целях (Тушева Г. М.). На рис. 9 в механизме шарнирного четырехзвенника кривошип 1 вращается с угловой скоростью w1=w, O1A=AB=l. Связав подвижную систему отсчета с кривошипом 1, найти для заданного положения механизма кориолисово ускорение точки В звена 2.
На рис. 10 круговой конус с прямым углом при вершине и радиусом основания, равным R, катится без скольжения по горизонтальной плоскости так, что скорость центра его основания vc=v. По ободу основания конуса движется точка М со скоростью u. Найти величину кориолисова ускорения для заданного положения точки М.