Was born in 1959 in Moscow, specialist in the field of partial differential equations and spectral properties of differential operators. He graduated from the Faculty of Computational Mathematics and Cybernetics, Lomonosov Moscow State University in 1981, listened to lectures of outstanding scientists A.N. Tychonov, A.A. Samarskii, N.S. Bakhvalov, V.A. Ilyin, L.N. Korolev. He have postgraduate studies at the Faculty of Computational Mathematics and Cybernetics, Lomonosov Moscow State University, specialty 01.01.02 in 1984 (supervisor - Prof., Dr. Sc. L. A. Muravei), Ph. D. degree (physical and mathematical sciences) in the specialty 01.01.02 in 1985 in the Dissertation Council of the Steklov Mathematical Institute Russian Academy of Sciences, Dr. Sc. degree (physical and mathematical sciences) in the specialty 01.01.02 in 1999 in the Dissertation Council of the Steklov Mathematical Institute Russian Academy of Sciences.
The scientific directions are stabilization of solutions of nonstationary boundary value problems, spectral theory of differential operators, singularly perturbed spectral problems, control problems of heat and diffusion processes, asymptotic expansions of solutions.
The scientific research is carried out with the Moscow State University. M.V. Lomonosov Moscow State University, Department of Differential Equations of the Faculty of Mechanics and Mathematics (Prof., D.Sc. I.V. Astashova) and Plekhanov Russian Economic University, Department of High Mathematics.
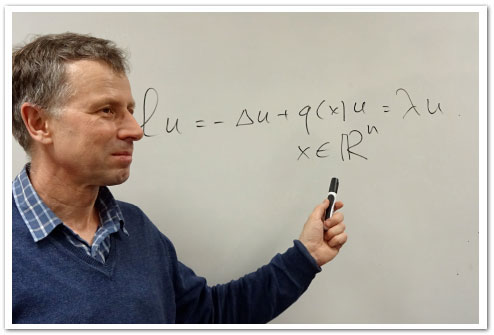 Filinovsky A.V. is the author of more than 100 papers on various problems of the qualitative theory of partial differential equations and spectral analysis of differential operators, two students passes Ph.D. defence. He is one of the supervisers of the weekly Interuniversity scientific seminar on the qualitative theory of differential equations (co-supervisor is Dr. Sc. I.V. Astashova), who collects researchers in the field of qualitative theory of differential equations, spectral analysis and applications (works since 2002).
Filinovsky A.V. is the author of more than 100 papers on various problems of the qualitative theory of partial differential equations and spectral analysis of differential operators, two students passes Ph.D. defence. He is one of the supervisers of the weekly Interuniversity scientific seminar on the qualitative theory of differential equations (co-supervisor is Dr. Sc. I.V. Astashova), who collects researchers in the field of qualitative theory of differential equations, spectral analysis and applications (works since 2002).
Filinovsky A.V. studied the problems of stabilization to solutions of nonstationary problems for hyperbolic and strongly hyperbolic equations in domains with compact and noncompact boundaries, including equations with nonuniformly elliptic operators. For the first time, the nature of the energy-to-infinity scattering in regions with noncompact boundaries star-shaped with respect to vector fields was studied and the structure of the energy wave front was investigated. It was developed the method for investigating to nonstationary problems is based on the estimates of the resolvent of elliptic operators with respect to the spectral parameter in the upper half-plane, also various variants of such estimates were obtained.
The spectral properties of elliptic boundary value problems in unbounded domains were investigated, while for the Dirichlet problem for an elliptic operator of high order were found the sufficient conditions to the continuity of the spectrum. The spectral properties of families of non-uniformly elliptic operators are studied, and the question of the transition from the discrete spectrum to the continuous one is studied.
A series of results on the limit behavior of the discrete spectrum of singularly perturbed boundary value problems is obtained, and the behavior of spectral projectors is investigated. These results are based on the established theorems on perturbations of abstract operators.
An important place in research is occupied by extremal problems for partial differential equations. There are the problems of spectral optimization, control problems to heat and diffusion processes. These problems were found numerous practical applications for the optimal realization of gettering processes and microclimate control in industrial greenhouses.
The review of the results is contained in the following books:
1) Astashova I.V., Ezhak S.S., Karulina E.S., Nikishkin V.A., Telnova M.Yu., Filinovsky A.V. Qualitative properties of solutions of differential equations and related problems of spectral analysis M.: UNITY-DANA, 2012, ISBN 978-5-238-02368-7.
2) Astashova I.V., Filinovskiy A.V., Kondratiev V.A., Muravei L.A. Some Problems in the Qualitative Theory of Differential Equations. J. of Natural Geometry, 2003, V. 23, no. 1-2, pp. 1-126, ISSN 0963-2654.
Web resources:
http://www.mathnet.ru/rus/person8448
http://www.ams.org/mathscinet/search/author.html?return=viewitems&mrauthid=223848
https://zbmath.org/authors/?q=au%3A%22filinovskii%2C%20a%2A%20v%2A%22





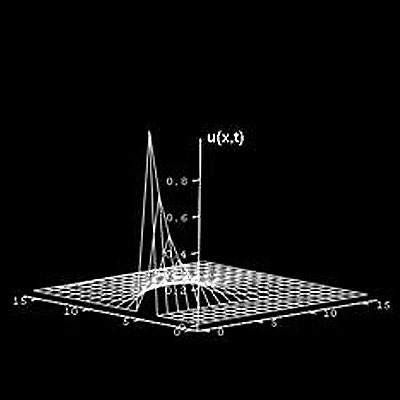 The Seminar gathers researchers in the field of qualitative theory of differential equations, spectral analysis and applications.
The Seminar gathers researchers in the field of qualitative theory of differential equations, spectral analysis and applications.


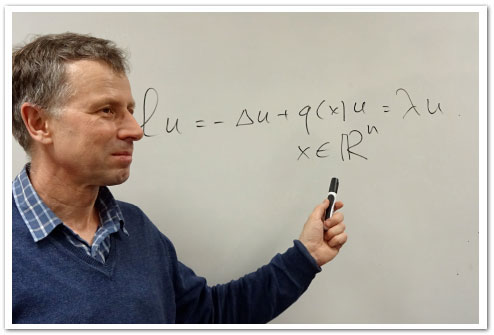 Filinovsky A.V. is the author of more than 100 papers on various problems of the qualitative theory of partial differential equations and spectral analysis of differential operators, two students passes Ph.D. defence. He is one of the supervisers of the weekly Interuniversity scientific seminar on the qualitative theory of differential equations (co-supervisor is Dr. Sc. I.V. Astashova), who collects researchers in the field of qualitative theory of differential equations, spectral analysis and applications (works since 2002).
Filinovsky A.V. is the author of more than 100 papers on various problems of the qualitative theory of partial differential equations and spectral analysis of differential operators, two students passes Ph.D. defence. He is one of the supervisers of the weekly Interuniversity scientific seminar on the qualitative theory of differential equations (co-supervisor is Dr. Sc. I.V. Astashova), who collects researchers in the field of qualitative theory of differential equations, spectral analysis and applications (works since 2002).
